Vor nun bald zwei Jahren habe ich mich schon einmal mit der Frage beschäftigt, ob Vorlesungen überholt sind. Inzwischen ist einiges Wasser die Oker vor meinem Büro entlanggeflossen, ich habe ein Hochschuldidaktik-Programm beinahe komplett absolviert und auch Praxiserfahrung gesammelt. Nun zaudere ich ein wenig, dieses große Fass anzustechen, denn es ist schon so viel dazu gesagt und geschrieben worden – und diskutieren kann man sicher endlos. Da aber gerade im Blog von Christian Spannagel das Thema erneut aufkam und ich außerdem über einen brandaktuellen Artikel von Louis Deslauriers, Ellen Schelew und Carl Wiemann gestolpert bin, schneide ich das Thema noch einmal an – wohl wissend, dass ich dabei einige Punkte offen lasse.
Begeben wir uns in die Mitte des 15. Jahrhunderts: Bücher kosten ein kleines Vermögen, weil sie entweder per Hand abgeschrieben werden oder über umständliche Verfahren in Druck gehen. Universitäten hüten die Schätze in ihren Bibliotheken, Professoren lesen in Vorlesungen aus diesen Büchern vor (daher der Name) und ergänzen die Texte durch eigene Kommentare. Die Studierenden schreiben stumm aber fleißig mit, und zur damaligen Zeit war das sicher eine effiziente Form, das geschriebene Wort zu Lernzwecken zu verbreiten.
Seit damals gab es allerdings ein paar Erfindungen, etwa den Buchdruck mit beweglichen Lettern, der Bücher für praktisch Jedermann erschwinglich machte, Kopierer oder das Internet. Allein um Inhalte zu verbreiten, bedarf es einer Vorlesung (hier im wahrsten Sinne des Wortes) also eigentlich nicht mehr. Den Stoff kann jeder selbst nachlesen oder mitunter auch in Hörbuch- oder Videoform genießen und dann sogar selbst festlegen, wo, wann und in welchen Häppchen er sie sich zu Gemüte führt. Zum Glück ist reines Vorlesen inzwischen wohl die Ausnahme, obwohl ich auch davon gehört, dass das noch mancherorts praktiziert wird. Heute dominiert an Universitäten mit Abstand der freie Vortrag der Dozenten (und in Seminaren setzt sich das oft bei den Studierenden fort). Inzwischen habe ich auch solche Frontalbeschallung in Grenzen schätzen gelernt, aber, großes Aber, nicht permanent und als einziges Mittel. Als Phase von etwa 20 Minuten mit klarem Lernziel, einverstanden. Bitte im Wechsel mit wirklichen Gesprächen, die zum Denken anregen, nicht nur Pseudozwischenfragen. Bitte im Wechsel mit Phasen, in denen man auch selbst etwas machen kann. Bitte…
Also, wenn Vorträge gut gemacht sind (sind sie leider selten, ich kann das auch nicht sonderlich gut), dann hält man sie auch mal 90 Minuten lang aus. Den Vortrag aber generell als DIE Methode zu benutzen, immer und überall, das stelle ich infrage. Bitte, liebe Dozenten, nutzt die knappe und wertvolle Präsenzzeit doch nicht nur für Monologe.
Wenn ihr meint, dann käme „hinten doch nichts mehr raus“, schaut euch vielleicht den Artikel von Deslauriers, Schelew und Wieman an (Improved Learning in a Large-Enrollment Physics Class). Das ist auch nur eine einzige Fallstudie, sicher nicht verallgemeinerbar, aber schaut sie euch doch bitte an. Was haben die drei gemacht?
Ein Kurs zur Quantenmechanik wurde in zwei fast gleich große Gruppen eingeteilt (jeweils etwa 270 Studierende) und beide zu je drei Stunden die Woche in einem Hörsaal mit fester Bestuhlung unterrichtet. Es gab in beiden Gruppen dieselben Hausaufgaben, Übungen usw. Beide Gruppen nahmen an denselben Prüfungen teil, zwei semesterbegleitend und eine abschließend. Beide Gruppen wurden elf Wochen lang von erfahrenen Dozenten mit guten Evaluationen im bekannten Vorlesungsmodus mit PowerPoint inklusive Beispielproblemen und Demonstrationen bearbeitet. Beide Gruppen unterschieden sich im Mittel bis zum Ende dieses Zeitraums kaum, was Leistung, Anwesenheit oder Engagement anging. Das überraschte die Autoren des Artikels, denn die Dozenten hatten recht unterschiedliche Persönlichkeiten gehabt.
Nun aber zum spannenden Teil: In Woche zwölf blieb in der Kontrollgruppe fast alles beim Alten. Der Dozent machte weiter wie gehabt, allerdings sollten nun die Unterrichtseinheiten durch Lesen relevanter Texte vorbereitet werden. In der Experimentalgruppe wechselte der Dozent. Der neue hatte weniger Lehrerfahrung vorzuweisen, gestaltete die Veranstaltungen aber abwechslungsreicher, beispielweise mit verschiedenen Aufgaben zur Vorbereitung auf die Sitzung, mit Kleingruppenarbeiten und Diskussionen. Es wurde zu Beginn auch kurz Zeit dafür verwendet zu erläutern, warum man die jeweils gewählte Methode nutzte.
In der Folgeveranstaltung wurde in beiden Gruppen derselbe Test geschrieben, der zuvor entworfen worden war und zwölf Fragen enthielt. Die Kontrollgruppe hatte in den drei Stunden den Stoff für alle zwölf Fragen behandelt, in der Experimentalgruppe konnten aus Zeitgründen nur die Inhalte für elf Fragen abgedeckt werden. Ergebnis: Die Kontrollgruppe erreichte im Mittel 41% der möglichen Punkte, die Experimentiergruppe 74% (durch bloßes Raten hätte man im Mittel 23% erhalten). Das Fragebogen-Feedback, das nach dem Kurs von den Studierenden eingeholt wurde, fiel ebenfalls sehr positiv aus.
Wie bereits angedeutet, diese einzelne Fallstudie beweist gar nichts. Ich hätte da auch verschiedene Ansatzpunkte für Kritik: War der Wechsel des Dozenten für den Unterschied verantwortlich (obwohl er eigentlich weniger praktische Lehrerfahrung besaß)? Hat allein die Beschäftigung mit den Studierenden dafür gesorgt, dass die Ergebnisse besser ausgefallen sind? Warum wurde die Experimentalgruppe nur eine einzige Woche lang anders unterrichtet? Wieso wurde das Experiment noch nicht wiederholt? Was sagen die verwendeten Multiple-Choice-Tests schon aus? Und so weiter, und so fort. Aber vielleicht ist doch wenigstens ein bisschen was dran…
Update: Wer die obigen Ausführungen gelesen hat, wird an dem zweifeln, was in DIE ZEIT dazu geschrieben wurde: Hier rein, da raus.
Update 2: Ein Kommentar von Philip Aschermann, Student an der TU Braunschweig: Universitäten sollten endlich die Vorlesung abschaffen – ein Kommentar.

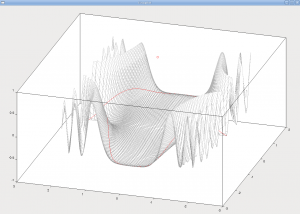
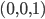 eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel
eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel 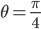 zur „Horizontalen“ um die vertikale Achse, die durch
zur „Horizontalen“ um die vertikale Achse, die durch 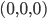 und
und 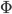 zurück und beschreibe schließlich im
zurück und beschreibe schließlich im 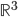 eine geschlossene Kurve.
eine geschlossene Kurve.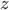 mit
mit 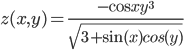 repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels
repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels  Unter dem Schlagwort Enterprise 2.0 wird gerade viel diskutiert und geforscht: Was bedeuten soziale Medien für Unternehmen? Lassen sich innerbetriebliche Strukturen und Prozesse damit verbessern? Wie ändert sich die Unternehmenskommunikation nach außen? Oder vielleicht: Warum ändert sie sich nicht? Brauchen Unternehmen einen Chief Listening Officer, damit den Kunden auch mal wirklich zugehört wird (Anleihe bei Gerald Fricke)?
Unter dem Schlagwort Enterprise 2.0 wird gerade viel diskutiert und geforscht: Was bedeuten soziale Medien für Unternehmen? Lassen sich innerbetriebliche Strukturen und Prozesse damit verbessern? Wie ändert sich die Unternehmenskommunikation nach außen? Oder vielleicht: Warum ändert sie sich nicht? Brauchen Unternehmen einen Chief Listening Officer, damit den Kunden auch mal wirklich zugehört wird (Anleihe bei Gerald Fricke)?